搜索树数据结构支持许多动态集合操作，包括SEARCH（查询）、MINIMUM（最小值）、MAXIMUM（最大值）、PREDECESSOR（前驱）、SUCCESSOR（后继）、INSERT（插入）、DELETE（删除）。因此我们使用一棵搜索树既可以作为一个字典又可以作为一个优先队列。

定义

　　对任何结点x，其左子树中的关键字最大不超过x.key，其右子树中的关键字最小不低于x.key。（如图）

　　

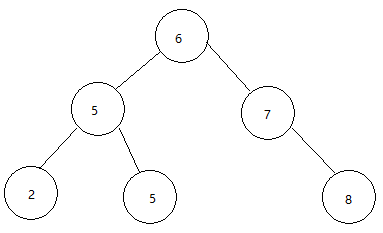
　　对于二叉树可以用其简单的方式来遍历。如先序遍历，中序遍历，后序遍历。（这里不进行讲解）

树的存储（SAVE）&初始化（INIT）

　　存储

　　在学习二叉搜索树之前我们先了解一下怎么存储树，用的是C++代码，网上的代码都是基于类的。并且对于C++的指针开空间说明的并不清楚。在上一篇文章中，我介绍了一种存储二叉树结点的方式（链表式），这里我们改进一下。

struct node //结点{    int value; //关键字    node* parent; //父结点    node* left; //左子    node* right; //右子}* root; //定义一个全局根

　　初始化

　　赋空自然是初始化要做的事情，不过在C++11中，为了避免老版本的NULL的问题（自行百度），加入了一个新的赋空方式nullptr，但是因为我用的编译器版本过低不支持C++11新特性，所以在这里我还是用的NULL，最好是用0赋空。

node* Tree_createNode(int value){    node* p = (node*)malloc(sizeof(node)); //结构体指针开空间    p->value = value; //赋值    p->parent = 0; //赋空    p->left = 0; //赋空    p->right = 0; //赋空    return p;}

插入（INSERT）

　　在学习树用法之前呢，我们先要了解一下怎么构树，说白了就是插入。

　　而插入也不是盲目的瞎放，我们要保证其二叉搜索树的性质来进行插入操作。

void Tree_Insert(int value){    if (!root)    {        root = Tree_createNode(value); //如果根不存在，创建        return;    }    node* curNode = root; //当前结点位置    node* insertNode = NULL; //要插入结点的父结点    node* p = Tree_createNode(value); //要插入结点    while (curNode) //找到插入结点的父结点（既子结点为空）    {        insertNode = curNode;        if (value < curNode->value)            curNode = curNode->left;        else            curNode = curNode->right;    }    p->parent = insertNode; //设置父结点    if (value < insertNode->value) //判断插入左子，还是右子        insertNode->left = p;    else        insertNode->right = p;}

查询（SEARCH）

　　SEARCH

　　我们经常需要查找一个存储在二叉搜索树上的关键字。设树的高度为h的话，查询的最坏时间为O（h）。

　　输入一个指向根的指针和一个关键字，如果这个结点存在则返回次结点，否则返回NULL。

　　代码其实跟插入是相同的思想。

node* Tree_Search(node* p, int value) //查找{    if (!p || value == p->value) //如果指针为空或找到，返回p        return p;    if (value < p->value)        return Tree_Search(p->left,value);    else        return Tree_Search(p->right,value);}

　　最大关键字（MAXIMUM）和最小关键字（MINIMUM）元素

　　了解二叉搜索树的思想就能想到，很简单，最小值就是一直找其左子，知道找到不到为止（最大值同理）。

node* Tree_Minimum(node* p) //查找最小值{    if (!p->left) return p;    Tree_Minimum(p->left);}node* Tree_Maximum(node* p) //查找最大值{    if (!p->right) return p;    Tree_Minimum(p->right);}

　　后继和前驱（SUCCESSOR&PREDECESSOR）

　　所谓前驱和后继是相对于遍历方式来说的，不过在二叉搜索树中比较特殊，因为二叉搜索树的中序遍历就是从小到大输出。所以相对于中序遍历的前驱和后继自然就是相邻的两个值。

　　后继有两种情况：

1. 有右子树，就找到其右子树为根的最小关键字就好，就是对右子调用MINIMUM。
2. 右子树为空且有一个后继y，那么y就是p的最底层祖先，并且y的左孩子也是p的一个祖先。（p为当前结点，y为后继结点）

node* Tree_Successor(node* p) //查找后继{    if (p->right) return Tree_Minimum(p->right);    node* y = p->parent;    while(y && p == y->right)    {        p = y;        y = y->parent;    }    return y;}

删除（DELETE）

　　有了插入自然也少不了删除的存在，相对于插入来说，删除较为复杂。

　　对于二叉搜索树中删除一个结点的整个策略分为三种基本情况（我们把删除结点设为z）：

• 如果z没有孩子结点，那么知识简单的将它删除，并修改它的父节点，用NULL作为孩子来替换z。
• 如果只有一个孩子，那么将这个孩子提升到树中z的位置上，并修改z的父结点，用z的孩子来替换z。
• 如果z有两个孩子，那么找z的后继y（一定在z的右子树上），并让y占据树中z的位置。z原来右子树部分成为y的新的右子树，并且z的左子树成为y的新的左子树。

　　对于第二种情况的示意图（左子同理）

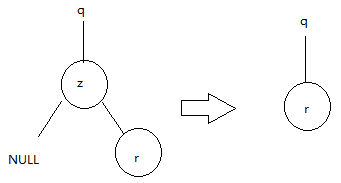
　　对于第三种情况的示意图分两种情况

　　1.右子直接为其删除结点z的后继

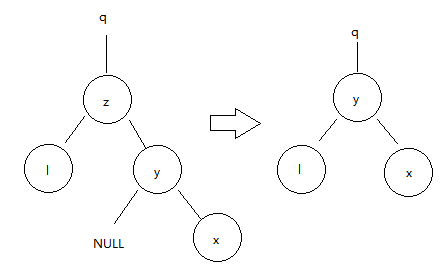
　　2.右子并非为其删除结点z的后继，则要找其z的后继。

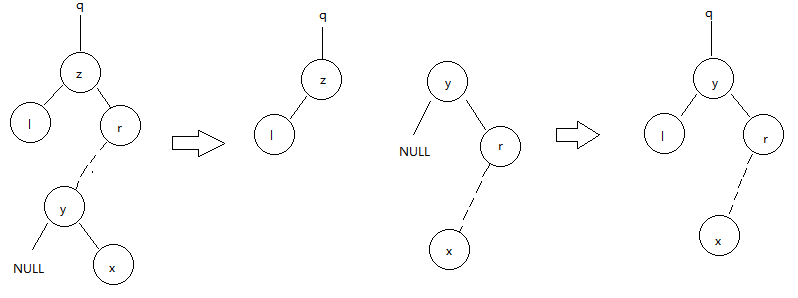
　　从上图可以看出，不管哪种删除操作都有一个共同特征，移动子树，所以我们定义一个过程TRANSPLANT。基本思想就是用另一颗子树替换一棵子树并成为其父结点的孩子结点。

node* Tree_Transplant(node *u, node *v) //将一棵以v为根的子树，替换一棵以u为根的子树{    if (!u->parent) //处理树根的情况    {        root = u;    }    else if (u == u->parent->left) //u为其左孩子    {        u->parent->left = v;    }    else //u为右孩子    {        u->parent->right = v;    }    if (v) //v不为空，则将v的父亲指向u的父亲    {        v->parent = u->parent;    }}

　　我们利用TRANSPLANT操作，从二叉搜索树中删除结点z的删除过程：

node* Tree_Delete(node *z) //删除操作{    if (!z->left) //左子树为空，对应第二种情况    {        Tree_Transplant(z,z->right);    }    else if (!z->right) //同上    {        Tree_Transplant(z,z->left);    }    else //第三种情况    {        node *y = Tree_Minimum(z->right);        if (y->parent != z) //第三种情况中的第二种情况，分成两个子树        {            Tree_Transplant(y,y->right);            y->right = z->right;            y->right->parent = y;        }        Tree_Transplant(z,y);        y->left = z->left;        y->left->parent = y;    }}

 （完）     如有问题请留言，只要看到一定回复。